Backtesting a Simple Stock Trading Strategy: Part 3
Note: This post is NOT financial advice! This is just a fun way to explore some of the capabilities R has for importing and manipulating data.
In a previous post, I examined a simple stock trading strategy: Find the high point over the last 200 days, and buy the stock if it’s been less than 100 days since that high. Otherwise, have no position.
What if we use different parameters than 200-day high and hold 100 days? How will that affect our strategy? First of all, we have to reload the data for the S&P 500 index and re-define the functions used to implement our strategy.
set.seed(42)
#Get Data
library(quantmod)
getSymbols('^GSPC',from='1900-01-01')
#> [1] "GSPC"
myStock <- Cl(GSPC)
bmkReturns <- dailyReturn(myStock, type = "arithmetic")
#Apply our strategy to tomorrows returns
#Today's close to tomorrow's close
myReturns <- Next(bmkReturns)
myReturns[nrow(myReturns)] <- 0
#Functions
daysSinceHigh <- function(x, n){
apply(embed(x, n), 1, which.max)-1
}
Next, we must decide the range of parameters we wish the test for our strategy. I’ve decided to use a “grid search” to thoroughly examine the parameter space. Somewhat arbitrarily, I’ve decided to test the values from 5-500, by 5, for both parameters. This gives us 100 possible values for each parameter, or 10000 total. Good thing the “daysSinceHigh” function is pretty fast!
Because my processing power is limited, I’m only going to look at every 5th value in this parameter space. The first order of business is to calculate a matrix containing each n-Day high series, where the first column is the number of days since the 5-day high, the second column is the number of days since the 10-day high, etc. This matrix has 100 columns:
highs <- seq(5,500,by=5)
highMatrix <- matrix(data=NA,nrow=length(myStock),ncol=length(highs))
colnames(highMatrix) <- highs
for (nHigh in highs) {
out <- daysSinceHigh(myStock,nHigh)
out <- c(rep(NA,nHigh-1),out)
highMatrix[,as.character(nHigh)] <- out
}
head(na.omit(highMatrix))
#> 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 125 130 135 140 145 150 155 160 165
#> [1,] 0 9 14 14 14 14 14 38 44 48 53 53 63 68 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71
#> [2,] 1 1 14 15 15 15 15 39 43 49 54 54 64 69 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72
#> [3,] 2 2 13 16 16 16 16 39 44 49 54 55 55 69 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73
#> [4,] 0 0 14 17 17 17 17 17 41 48 54 56 56 69 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74
#> [5,] 1 1 13 18 18 18 18 18 42 49 54 57 57 67 72 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75
#> [6,] 2 2 14 19 19 19 19 19 43 49 53 58 58 68 73 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76
#> 170 175 180 185 190 195 200 205 210 215 220 225 230 235 240 245 250 255 260 265 270 275 280 285 290 295 300 305
#> [1,] 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71
#> [2,] 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72
#> [3,] 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73
#> [4,] 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74
#> [5,] 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75
#> [6,] 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76
#> 310 315 320 325 330 335 340 345 350 355 360 365 370 375 380 385 390 395 400 405 410 415 420 425 430 435 440 445
#> [1,] 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71 71
#> [2,] 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72 72
#> [3,] 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73 73
#> [4,] 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74 74
#> [5,] 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75 75
#> [6,] 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76 76
#> 450 455 460 465 470 475 480 485 490 495 500
#> [1,] 71 71 71 71 71 71 71 71 71 71 71
#> [2,] 72 72 72 72 72 72 72 72 72 72 72
#> [3,] 73 73 73 73 73 73 73 73 73 73 73
#> [4,] 74 74 74 74 74 74 74 74 74 74 74
#> [5,] 75 75 75 75 75 75 75 75 75 75 75
#> [6,] 76 76 76 76 76 76 76 76 76 76 76
Next, I make a list with 100 elements. Each element represents a holding period, which I will apply to a copy of the “n-Day high matrix” from the previous step. For example, the 1st element in the list is a matrix representing a 5-day holding period. The first column in this matrix represents buying at the 5-day high, and holding for 5 days. This is equivalent to buy-and-hold. The second column represents buying at the 10-day high, and holding for 5 days. The third column represents buying at the 15-day high and so on. I repeat this process for each element in the 100-matrix list, which gives us an object representing every possible permutation of our strategy.
#Calculate Returns for various combinations of n-day highs and holding periods
holds <- seq(5,500,by=5)
returnsList <- list(NA)
for (nHold in holds) {
out <- ifelse(highMatrix<=nHold,1,0)
out <- ifelse(is.na(out),0,out)
out <- sweep(out,MARGIN=1,myReturns,`*`)
returnsList[[as.character(nHold)]] <- out
}
returnsList[[1]] <- NULL
It is then a relatively easy thing to calculate the returns associated with each permutation of the strategy, by using the “sweep” function to multiply each column of each matrix by the daily returns for our stock
#Calculate Cumulative Returns for various scenarios
cumRet <- as.list(rep(NA,length(returnsList)))
i=1
for (returnMatrix in returnsList) {
cumRet[[i]] <- apply(returnMatrix,MARGIN=2,function(x) prod(1 + x) - 1)
i <- i+1
}
cumRet <- unlist(cumRet)
bmkRet <- prod(1 + bmkReturns) - 1
exRet <- cumRet-bmkRet
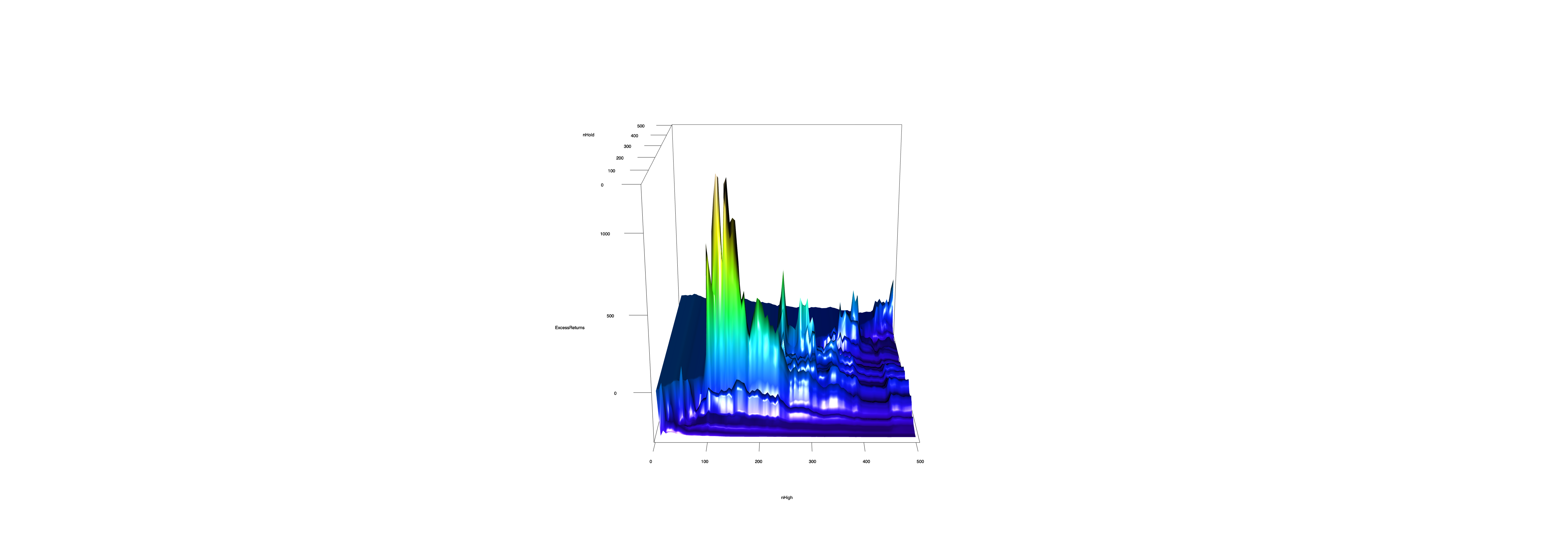
Now we have a list of matrices of returns. Each column of a matrix represents the returns of our strategy, using a different set of parameters. This allows us to calculate cumulative returns for each set of parameters, and make a nifty graph that shows the relationship between nHigh, nHold, and returns.
#Custom Color Ramp Function
range01 <- function(x)(x-min(x))/diff(range(x))
cRamp <- function(x){
cols <- colorRamp(topo.colors(10))(range01(x))
apply(cols, 1, function(xt)rgb(xt[1], xt[2], xt[3], maxColorValue=255))
}
#Plot
Data <- data.frame(expand.grid(nHigh=highs,nHold=holds),exRet=exRet)
Data <- Data[Data$nHold<=Data$nHigh,]
plot(Data[,c(1,2)],col=cRamp(Data$exRet),pch=19,lwd=2)
This graph uses a custom color ramp function, which was created by Andrie on StackOverflow. The color of each point in the corresponds to how high the returns are at that point. The X axis is number of days to use for the nHigh, and the yAxis is the number of days to use for nHold. As you can see, 100 days seems to be a solid holding period across many values of nHigh, but by using a different value of nHigh, we could increase returns substantially.
Of course, just because these values worked in the past doesn’t mean they will work in the future. Still, it’s good to see that our arbitrary parameters (which performed well in the last post), fall inside a wide range of parameters that yield a positive return for our strategy. This brings up an interesting question: how DO we select parameters for our strategy? How can we tell how well our parameter selection strategy would have performed in the past, given that we’ve optimized our selection based on of our knowledge of the past?
For homework, think about how overfitting and cross-validation apply to this problem…
BONUS CODE: This creates some nifty 3D charts, using the rgl library.
library(rgl)
ExcessReturns <- matrix(exRet, length(highs), length(holds))
nHigh <- highs
nHold <- holds
persp3d(x=nHigh, y=nHold, z=ExcessReturns, box=FALSE, col=cRamp(ExcessReturns))